This website uses cookies, Web Storage technology and similar, among others in order to ensure maximum convenience in using our website. If you do not change the settings, the files will be saved in the memory of your device. You can read more in privacy policy.
Triangle calculator -height, area, perimeter, sides
Triangle calculator will help you calculate the area, perimeter, sides, height, angles of any triangle, right triangle and equilateral.
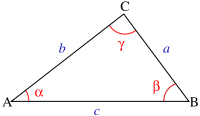
a, b, c - side lengths;
ha, hb, hc - heights from sides a, b, c;
α, β, γ - angles opposite the sides a, b, c;
S - area;
R - radius of the circumscribed circle;
r - radius of the inscribed circle;
p - half the perimeter of the triangle;
 |
 |
 |
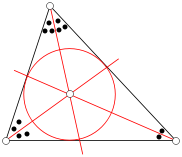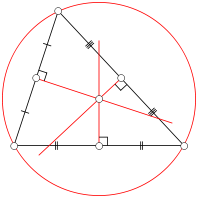
| Okrąg opisany | Okrąg wpisany |
a, b, c - side lengths;
ha, hb, hc - heights from sides a, b, c;
α, β, γ - angles opposite the sides a, b, c;
S - area;
R - radius of the circumscribed circle;
r - radius of the inscribed circle;
p - half the perimeter of the triangle;
Have you counted - click like and share
Have you counted - click like and share
Users of this calculator also used
Vernam cipher - encoder / decoder
Vernam cipher online encoder and decoder. Encrypt and decrypt any cipher created in a Vernam cipher.
ROT47 cipher - encoder / decoder
ROT47 cipher online encoder and decoder. Encrypt and decrypt any cipher created in a ROT47 cipher. You can use any shift and additionally a key for more precise text encoding.
Rail Fence, Zig-Zag - encoder / decoder
Rail Fence, Zig-Zag cipher online encoder and decoder. Encrypt and decrypt any cipher created in a Rail Fence, Zig-Zag cipher.
Weighted arithmetic mean calculator
With this calculator you will calculate the weighted arithmetic mean.
Voltage drop calculator for single-phase and three-phase circuits
With this calculator you will calculate the voltage drops for single-phase and three-phase AC circuits calculated from active power.
You will also calculate cable length, conductor diameter, conductor cross-sectional area, phase or line voltage or active power.
Isosceles trapezoid - diagonals, height, area, perimeter, sides
Isosceles trapezoid calculator will help you calculate diagonal of the isosceles, the side length, height, area, perimeter and the radius of the circumscribed circle of the isosceles.
Vertical projectile motion - speed, time, height
With this calculator, you can calculate the velocity of a body thrown vertically after a specified time and the initial velocity given to the body. You will also calculate the time elapsed from the moment of the throw to reach a certain speed, the time the body flies to the return to the place of the throw and the time after which the body reaches its maximum height. The calculator will also help you calculate the height at which the body is located after a certain time and will calculate the maximum height that the body will reach. The calculator also allows you to estimate the gravitational acceleration which can be useful in determining where the body was thrown.